Моделирование

Концепция моделирования

Креативность научных исследований, проводимых НПО РИТ, связана с концепцией моделирования. Развитие концепции, основанной на понятии «имитационная модель» является понятие «имитационная система моделирования». Термин корректный, и с точки зрения здравого смысла, и оказался удобным для обозначения того объекта, который возникает, если, во-первых, отобразить математическую модель на совокупность программ, обеспечивающих «должную» степень удобства при общении с машиной в процессе проведения вычислительного эксперимента. Вычислительный эксперимент как система в свой состав включает человеческий и технический факторы, совокупность методологических средств и процедур их взаимодействия. Одним из важнейших свойств вычислительного эксперимента является универсальность, которая позволяет легко переносить эту технологию на исследование других объектов. При этом самое известное физическое проявление универсальности – виртуальная реальность. Поэтому, с методологической точки зрения, вычислительный эксперимент рассматривается как человеко–машинная система с технологическими средствами получения выходной информации, необходимой для обслуживания специалистов в различных сферах человеческой деятельности. При этом большое внимание уделяется интенсивному поиску в области, так называемого, "некомандного" интерфейса, последнее связано с направлением, что сегодня носит название "виртуальная реальность".

Инструментальная составляющая моделирования

Модели оптимизации:

• Методы решения задач линейного программирования
• Метод решения задач нелинейного программирования
• Методы динамическое программирование
• Методы случайного поиска

Модели вычисления специализированных математических функций и решения линейных уравнений:

• Библиотека моделей расчета специализированных функций
• Библиотека методов решения линейных уравнений
• Модели численного интегрирования и дифференцирования

Автоматизированная подготовка исходных данных адаптированных к среде моделирования

• Аппаратный подход к решению задачи по автоматизированной подготовке данных;
• Создание САПР для подготовки исходных данных для проведения вычислительного эксперимента (подход основан на синтезе различных сред моделирования;

Системный подход к созданию современного методического аппарата реализации среды моделирования

Построение схемного решения по алгоритмическому представлению вычислительного процесса.

Онтология формирования технологической схемы разработки среды моделирования основывается на концепции процессно-ориентированного подхода и математическом аппарате теории графов. При описании построенного графа на языке описания аппаратуры вершины графа принимают вид аппаратных модулей, в которых определены входные шины данных и выходные, а рёбра являются самими шинами данных, через которые происходит прохождение информации по вычислительной системе. Архитектура построенной по такому графу вычислительной системе является полностью адекватной архитектуре процесса вычисления, что обеспечивает максимальную производительность реконфигурируемого вычислителя (архитектура под задачу). На определенном шаге методики предполагается выполнение трёх действий:

• построение графа временной зависимости по алгоритмическому описанию вычислительного процесса;
• построение графа информационной зависимости на основе графа временной зависимости;
• генерация схемного решения на основе графа информационной зависимости (рисунок 5.1).

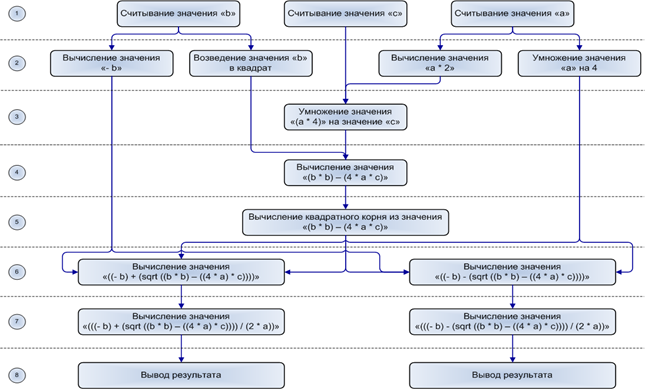
Вариант построения графа временной зависимости по исходному коду на языке высокого уровня может быть реализован по следующей схеме. Проводится препроцессорная обработка, лексический, синтаксический и семантический анализы исходного текста, в результате чего строится дерево синтаксического разбора. Как правило классический компилятор успешно выполняет эти стадии. Этот компилятор имеет модульную архитектуру, в которой каждая стадия выполняется отдельным модулем. Модули препроцессора, лексического анализатора и синтаксического анализатора зависимы от исходного языка программирования. При обработке добавляемого языка программирования эти модули должны быть написаны и заменить собой соответствующие модули. Модуль семантического анализа независим от исходного языка программирования и может использоваться для любого поддерживаемого языка программирования. Такая архитектура позволяет обрабатывать большой класс исходных языков программирования за счёт взаимозаменяемости модулей, зависимых от исходного языка программирования. Стадии, зависимые от исходного языка программирования, абстрагируют исходный код до описания алгоритма (дерево синтаксического разбора), которое является независимым от исходного языка программирования.

Моделирование сверх больших информационных сетей

Методика программно - аппаратного моделирования распределенных сетей на основе однородной вычислительной среды, реализованной в программируемых логических интегральных схемах

Рассматривая программно-аппаратный подход к построению модели вычислительной сети следует отметить, что разработанная среда моделирования состоит из системы универсальных вычислительных модулей (УВМ) объединенных высокоскоростной коммуникационной сетью. УВМ состоит из реконфигурируемого ресурса (ПЛИС) и ресурса оперативной памяти. Реконфигурируемый ресурс и ресурс оперативной памяти является основой для формирования виртуальной системы моделирования информационной сети. При этом реконфигурируемый ресурс состоит из структуры аппаратных процессоров, обеспечивающих обработку входного вектора данных и формирования выходного вектора данных, в соответствии с определенным функционалом преобразования. Ресурс оперативной памяти служит для размещения виртуальной системы данных и команд графа состояния моделируемой информационной сети. Разделение среды моделирования на реконфигурируемый ресурс и ресурс оперативной памяти необходимо для описания в оперативной памяти сверх больших информационных сетей и обеспечения максимально возможной скорости обработки информации аппаратными процессорами. Предлагаемая гетерогенная среда моделирования состоит из стандартных кластерных модулей, набора УВМ, высокопроизводительного коммутатора структуры связей, набора периферийных модулей. При этом основные вычисления переносятся на аппаратную часть, а сбор статистики, ее анализ и корректное отображение результатов ложится на программную интерфейсную часть. Основные достоинства данного подхода заключаются в том, что он позволяет достичь практически неограниченного параллелизма за счет наращивания аппаратуры, что предоставляет возможность моделировать сеть в режиме реального времени.

Методика программно – аппаратного моделирования распределенных сетей на основе аппаратных процессоров с виртуальной архитектурой потока команд и данных построенной на графе состояния

Задача построения программно – аппаратного модели распределенных сетей на основе аппаратных процессоров с виртуальной архитектурой потока команд и данных, ее формальная постановка и методы решения, отображаются на домен креативного формально - технологического класса. Особенностью технологии моделирования распределенных информационных сетей является то, что граф состояния сети имеет большое число узлов. Узел графа состояния соответствует определенному типу устройства (коммутатор, маршрутизатор, мост, повторитель, канал передачи данных, сервер). Для создания эффективных моделей сложных информационных сетей, среда моделирования представлена аппаратными компонентами, реализующими алгоритм работы моделируемого узла и командной, адресной и служебной информацией размещенной в секторах динамической памяти. Эта информация представляет собой пакет с командой, данными, служебной адресной, информацией необходимый для выбора соответствующего аппаратного процессора и реализации алгоритма его работы. Структура моделирующей среды состоит из пакетов с командой, данными служебной адресной, информацией расположенные в ОЗУ и системы иерархических аппаратных процессоров, обеспечивающих обработку соответствующего пакета в соответствии с его предназначением и расположенные в ресурсе ПЛИС.

Преимуществом использования аппаратного процессора является то, что в обработку поступает весь пакет и возможность практически неограниченного распараллеливания вычислительного процесса и отсутствие потока команд. Современная динамическая память DDR обладает высокой скоростью обмена данных. Для модулей DDR2 она составляет 5.3 гигабайта в секунду. Время сканирования динамического ОЗУ составляет 0.2 секунды. По предварительной оценке, в DDR2 модуле объемом памяти 1 гигабайт при длине пакета 100 байт, можно разместить до десяти миллионов узлов моделируемой сети. Принцип работы среды моделирования основан на процессе непрерывного сканирования динамического ОЗУ, формирования потока процессов, выборкой пакета с командой и данными, решения в соответствующем аппаратном процессоре с обратной записью результатов в динамическое ОЗУ. Данный подход позволяет эффективно моделировать сверхбольшие информационные сети, что обеспечило решение оптимизационной задачи связанной с максимизации количества элементов входящих в контур АСУ, при ограничениях на вычислительные ресурсы.

Модели динамической системы

Система проведения вычислительного эксперимента включает в себя модель объекта, в виде математических отношений, описывающую поведение реального объекта, эти отношения представляют в математических терминах концепцию отображения модели объекта исследования в среду моделирования. Для вывода математической модели в форме уравнений Лагранжа второго рода:

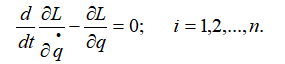
выделены обобщенные координаты системы, набор которых целиком зависит от характера взаимодействия тел. Обобщенные координаты, описывающие поведение динамической системы, разделены на угловые 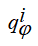и линейные 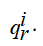. При введенных предположениях кинематика движения тел системы задается выражениями:

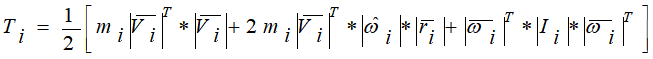
Обобщенные координаты и их производные по времени позволяют определить перемещения и скорости любого тела расчетной схемы, они в свою очередь – кинетическую и потенциальную энергии, а также диссипативную функцию рассеивания энергии:

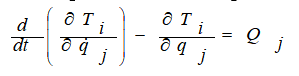
Кинетическая энергия в общем случае определяется выражением:

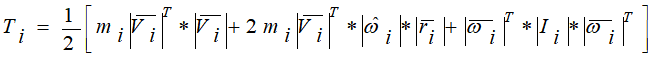
где 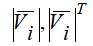вектор и транспонированный вектор «линейной» скорости i-го тела (данная форма представления позволяет алгоритмизировать процедуру построения уравнений движения);
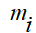масса i-го тела;
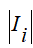тензор инерции i-го тела;
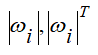вектор и транспонированный вектор угловой скорости i-го тела;
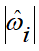кососимметричная матрица угловой скорости.

При этом основные методологические положения построения математической модели динамической системы обобщаются следующими пунктами:

• Выделяются тела, образующие механическую систему, определяется количество степеней свободы и выбираются обобщенные координаты.
• Строится древовидная структура, характеризующая расположение и взаимодействие тел между собой.
• Строится система дифференциальных уравнений второго порядка, состоящую из N*M уравнений, где N- количество обобщенных координат, а M- количество тел, образующих механическую систему.
• Решается система дифференциальных уравнений с учетом выбранных начальных условий одним из методов численного интегрирования для систем дифференциальных уравнений второго порядка метод Рунге-Кутты четвертого порядка. Следует отметить, что при каждом обращении к системе из уравнений движения, при численном интегрировании, для нахождения значений вторых производных от обобщенных координат необходимо решать систему линейных уравнений.